Compártelo:

Rating: 4.77/5. From 13 votes.

Please wait...

Contenido

1 Conjuntos Numéricos

Conjuntos Numéricos

Dentro de las matemáticas en general, y particularmente cuando estudias aritmética, necesitas entender los diferentes conjuntos numéricos y las relaciones que éstos guardan entre si.

En álgebra también es necesario comprender tales sistemas numéricos. A continuación les presento un mapa mental de los conjuntos numéricos.

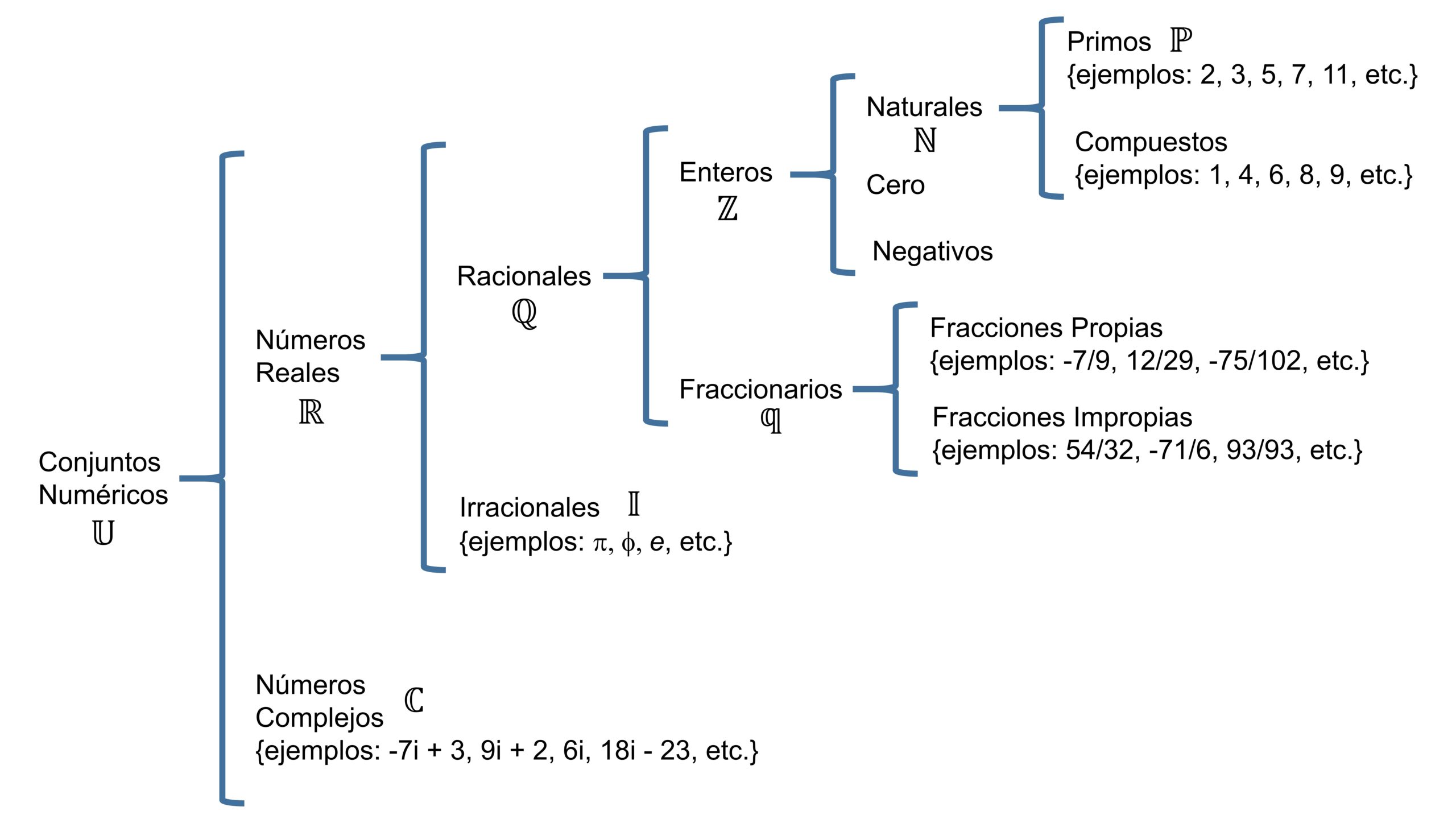
Los conjuntos numéricos están compuestos por dos grandes conjuntos llamados: Números reales y Números complejos.

Números Reales

Los números reales son cualquier número que te puedas imaginar de cualquier característica y propiedades. También el conjunto de los números reales se compone en dos grandes conjuntos numéricos: Números racionales y Números irracionales. Como ejemplos tenemos los siguientes.

$\mathbb R = \left\lbrace...-1672, \frac{-346}{23}, 0, 1.618033..., 2.718281828..., 3.141592654..., 5, \frac{17}{3}, 11,...\right\rbrace$

Números Racionales

Los números racionales son todos aquellos números que pueden ser representados por una fracción de dos números enteros. El resultado de la fracción puede ser infinita y puede tener secciones numéricas periódicas. Por ejemplo, el número racional 1/3 tiene resultado como sigue,

$\frac{1}{3} = 0.3333333333...$

o puesto con notación de periodicidad numérica,

$\frac{1}{3} = 0.\bar{3}$

Debido a que cualquier número que puede ser representado por una fracción de dos números enteros es un número racional, entonces podemos ver que los siguientes números pueden ser ejemplos de números racionales

$\mathbb Q = \left\lbrace-5 = \frac{-100}{20}, -1000 = \frac{-2000}{2}, 4 = \frac{8}{2}, ...\rigth\rbrace$

Números Enteros

Los números enteros pueden ser representados por la letra $\mathbb Z$ . A continuación tenemos algunos ejemplos.

$\mathbb Z = \left\lbrace...-1232, -129, -3, -2, 0, 24, 391, 10000,...\rigth\rbrace$

los anteriores solo son algunos ejemplos. Ahora podemos representarlos en forma de un conjunto abierto de la siguiente manera,

$-\infty < \mathbb Z < +\infty$

Números Naturales

Son los primeros números enteros que se considera que usaron las civilizaciones para poder entender el concepto de contar los objetos que los rodeaban. Van desde el número 1 hasta el infinito. El conjunto se representa en notación matemática de la siguiente manera,

$1 < \mathbb N < +\infty$

Números Primos

Los números primos son un conjunto de números con propiedades muy especiales. Solo son divisibles entre si mismos y entre el número 1. A continuación algunos elementos de los números primos,

$\mathbb P = \left\lbrace2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31,...\rigth\rbrace$

al inicio ves que el 2 es el único número primo par, todos lo demás primos son impares. Pero ojo, que no todos los números impares son primos. Por ejemplo, el caso del número impar 9. Este no es primo porque es divisible también entre 3, no solo entre 1 y 9. Si el número 9 solo fuera divisible entre 1 y 9 también hubiera sido primo, pero no lo es.

Números Compuestos

Los no primos, los números compuestos, todos los que no son números primos. Los que a parte de ser divisibles entre 1 y ellos mismos, también son divisibles entre 2, o 3, o 4 o cualquier otro número entero. A continuación represento algunos de los números compuestos,

$\mathbb P = \left\lbrace1, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18,...\rigth\rbrace$

también aquí ves que hay pares e impares.

Número Cero

Es un número muy particular que representa la ausencia de algo. En matemáticas representa una cantidad nula. Cero es nada, es ninguna cantidad de algo. Es la no existencia de números o cantidades de ciertas cosas en los problemas matemáticos. Es quitarle a una cantidad la propia cantidad. El cero es el centro de la recta numérica en el conjunto infinito de los números reales.

$-\infty...,0,...+\infty$

Números Negativos

Los números enteros negativos se encuentran a la izquierda del cero en la recta numérica. Las propiedades de los números enteros negativos son opuestas en signo únicamente a los enteros positivos. Un número entero negativo significa el número de saltos enteros que se dan a la izquierda a partir del cero para llegar a la posición de este en la recta numérica. A continuación la representación de los números enteros negativos,

$-\infty...,-200, -199, -198,...,-11, -10, -9,...,-5, -4, -3, -2, -1$

Números Fraccionarios

Los números fraccionarios pueden ser representados por dos tipos particulares de fracciones: Fracciones Propias y Fracciones Impropias.

A continuación la descripción de este tipo de números fraccionarios.

Fracciones Propias

Las fracciones propias son las fracciones cuyo numerador es inferior en valor absoluto al denominador, por ejemplo:

$..., \frac{-5}{7}, \frac{-7}{11}, \frac{-13}{24}, \frac{6}{7}, \frac{9}{12}, \frac{23}{76}, ...$

Fracciones Impropias

Las fracciones impropias son las fracciones en las que el numerador es superior al denominador en valor absoluto. Debido a esto, el denominador al menos cabe una vez en el numerador y por lo tanto una fracción impropia siempre se podrá representar como una fracción mixta.

Las fracciones mixtas se componen de una parte entera y una fracción propia.

A continuación algunos ejemplos de fracciones impropias,

$..., \frac{-32}{24}, \frac{-179}{178}, \frac{-13}{11}, \frac{12}{11}, \frac{19}{4}, \frac{163}{34}, ...$

Ejemplo: Representar una fracción impropia en fracción mixta.

$\frac{163}{34} = ?$

primero se preguntan cuántas veces cabe el 34 en el 163. Descubres que cabe 4 veces, y este 4 multiplicado por 34 es 136. Así que el numerador, 163, se parte en la suma 136 + 27,

$\frac{163}{34} = \frac{136 + 27}{34}$

luego se separan en dos fracciones,

$\frac{163}{34} = \frac{136}{34} + \frac{27}{34}$

y notaremos que en la primera la división es entera y es el 4 con la que obtuvimos el 136.

$\frac{163}{34} = 4 + \frac{27}{34}$

y finalmente este resultado se puede expresar de la siguiente manera conocida como fracción mixta,

$\frac{163}{34} = 4\frac{27}{34}$

nota que la fracción que acompaña al 4 es una fracción propia la cual es irreducible puesto que el 27 y el 34 no tienen un número entero en común que los divida simultáneamente.

Números Irracionales

Los números irracionales son todos aquellos números reales que no pueden ser representados por una fracción de dos números enteros.

Sus características son tan peculiares que tienen una cantidad infinita de dígitos después del punto decimal. Los ejemplos más típicos tienen que ver directamente con la naturaleza de manera curiosa e intrigante, como si la naturaleza estuviese gobernada por números irracionales. A continuación algunos ejemplos,

Ejemplo 1: El número pi ( $\pi$ )

El número $\pi$ es el número irracional más popular y significa el número de veces que cabe un diámetro de una circunferencia dentro del perímetro de la circunferencia. No importa que tan grande o tan pequeña sea la circunferencia, siempre la división del perímetro entre el diámetro siempre es el valor del número $\pi$ ,

$\pi$ = 3.1415926535897932384…

$\pi$ es el número que obedece la curvatura de una circunferencia y por eso lo vas a encontrar en todo problema geométrico en el que esté implicada la naturaleza circular.

Ejemplo 2: El número de Euler (e)

Se le conoce como la base del logaritmo natural y su valor es,

e = 2.718281828459045235360…

también se le conoce como constante de Napier porque fue utilizado por primera vez por el matemático escocés John Napier. Napier introdujo el concepto de logaritmo en el cálculo.

Ejemplo 3: El número áureo ( $\varphi$ )

El número áureo, conocido también como número de oro, número de Dios, razón divina, y muchos otros nombres se representa con la letra griega $\varphi$ en honor al escultor griego Fidias.

Puede ser calculado por la siguiente expresión,

$\varphi = \frac{1 + \sqrt{5}}{2}$

$\frac{1 + \sqrt{5}}{2} = 1.618033988749894...$

$\varphi \approx 1.618033988749894...$

es un número implicado directamente en la naturaleza de manera muy intrigante e interesante. Esta proporción se encuentra tanto en algunas figuras geométricas. Lo puedes encontrar en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, etc.

Números Complejos

Los números complejos es el conjunto numérico menos popular ya que se ven en las matemáticas avanzadas en cursos de bachillerato o hasta la universidad. El origen de este tipo de números es la raíz cuadrada del -1.

$\sqrt{-1} = i$

Los números complejos tiene una parte real y una parte imaginaria. Se definen de la siguiente manera,

$z = a + bi$

tenemos que “a” es la parte real y “b” la magnitud de la parte imaginaria.

Ejemplo: La suma de 2 números complejos

Sean z1 y z2 dos números complejos definidos de la siguiente manera,

z1 = 5 + 3i

z2 = -8 + 4i

la suma de estos dos números complejos es de la siguiente manera,

z1 + z2 = 5 + 3i + (-8 + 4i)

z1 + z2 = 5 + 3i – 8 + 4i

se agrupan las partes reales de ambos números complejos y también las dos partes imaginarias,

z1 + z2 = 5 – 8 + 3i + 4i

y obtenemos,

z1 + z2 = -3 + 7i

como pudiste darte cuenta, la suma de dos números complejos no es tan compleja. Se suman o restan partes reales al igual que se suman o se restan las partes imaginarias por separado para componer al nuevo número complejo. En la suma y resta de números complejos pueden pasar casos curiosos como que al sumar o restar dos números complejos el resultado sea un número real o sea un número puramente imaginario.

Examen 7. Conjuntos Numéricos

Si ya te sientes lista o listo para hacer el examen 7 de conjuntos numéricos entonces en la siguiente liga puedes acceder a este. Te va a pedir que te registres. De momento el registro es gratuito dándote acceso a resultados y un seguimiento a tu curso de álgebra.

Clase 7 de Álgebra – Conjuntos Numéricos

Conjuntos Numéricos